What is the Golden Ratio?
The Golden Ratio is known as the divine proportion and is supposed to be the most aesthetically pleasing ratio. It is defined as the point at which A+B:A is equal to A:B. Another way to write this is \[\frac{a+b}{a}=\frac{a}{b} =\Phi\]. People have been aware of it since the time of the Egyptians and it has been studied through the ages. The Greeks were responsible for much of the knowedge about the Golden Ratio. Euclid, one of the most influential mathematicians, was aware of it and wrote about it. He called it the Golden Mean and linked to the pentagram. Later Fibonacci, created the Fibonacci Sequence which has a relationship to the Golden Ratio, although is it debated whether he knew about this.
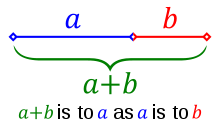
Methods of finding the Golden Ratio
The Golden Ratio is 1:1.6180339887498948482045868343656381...
The equation to find the Golden Ratio is \[\Phi=\frac{1+\sqrt{5}}{2}\].You can also approximate the Golden Ratio by dividing two consecutive numbers in the Fibonacci Sequence.
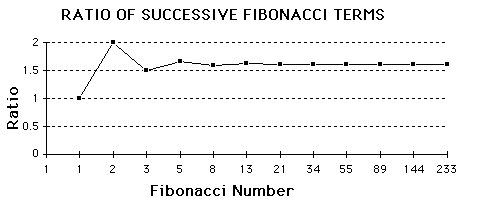
\(\Phi\)=1.6180339887...
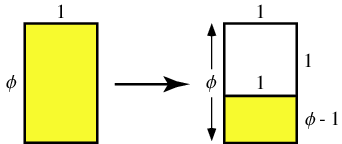To find the equation for the Golden Ratio start with the rectangle above and the Ratio of the length to the width \[\frac{\Phi}{1} = \frac{1}{\Phi-1}\]\[\frac{\Phi}{1}=\frac{1}{\Phi-1}\]
\[\frac{\Phi-1}{1}*\frac{\Phi}{1}=\frac{1}{\Phi-1}*\frac{\Phi-1}{1}\]
\[\frac{\Phi-1}{1}*\frac{\Phi}{1}=\frac{1}{\cancel{\Phi-1}}*\frac{\cancel{\Phi-1}}{1}\]
\[\Phi^2-\Phi=1\]
\[\Phi^2-\Phi-1=0\]
Now you can use the quadratic formula to solve the equation. \[\frac{-b\pm\sqrt{b^2-4ac}}{2a}\]
\[\frac{1\pm\sqrt{-1^2-4(1)(-1)}}{2(1)}\]
\[\frac{1\pm\sqrt{5}}{2}\]